Find All Solutions to Each of the Following Triabgles
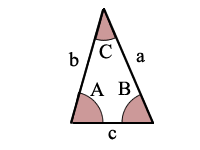
Triangle Figure
Angle-Side-Angle (ASA)
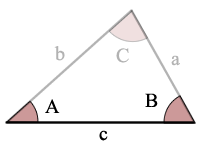
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle
Calculator Use
Each calculation option, shown below, has sub-bullets that list the sequence of methods used in this calculator to solve for unknown angle and side values including Sum of Angles in a Triangle, Law of Sines and Law of Cosines. These are NOT the ONLY sequences you could use to solve these types of problems.
- See also these Trigonometry Calculators:
- Law of Cosines Calculator
- Law of Sines Calculator
Solving Triangle Theorems
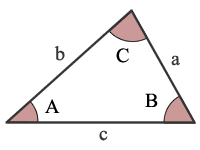
AAA is Angle, Angle, Angle
Specifying the three angles of a triangle does not uniquely identify one triangle. Therefore, specifying two angles of a tringle allows you to calculate the third angle only.
Given the sizes of 2 angles of a triangle you can calculate the size of the third angle. The total will equal 180° or π radians.
C = 180° - A - B (in degrees)
C = π - A - B (in radians)
AAS is Angle, Angle, Side
Given the size of 2 angles and 1 side opposite one of the given angles, you can calculate the sizes of the remaining 1 angle and 2 sides.
use the Sum of Angles Rule to find the other angle, then
use The Law of Sines to solve for each of the other two sides.
ASA is Angle, Side, Angle
Given the size of 2 angles and the size of the side that is in between those 2 angles you can calculate the sizes of the remaining 1 angle and 2 sides.
use the Sum of Angles Rule to find the other angle, then
use The Law of Sines to solve for each of the other two sides.
ASS (or SSA) is Angle, Side, Side
Given the size of 2 sides (a and c where a < c) and the size of the angle A that is not in between those 2 sides you might be able to calculate the sizes of the remaining 1 side and 2 angles, depending on the following conditions.
For A ≥ 90° (A ≥ π/2):
If a ≤ c there there are no possible triangles
Example:
If a > c there is 1 possible solution
- use The Law of Sines to solve for angle C
- use the Sum of Angles Rule to find the other angle, B
- use The Law of Sines to solve for the last side, b
- Example:
For A < 90° (A < π/2):
If a ≥ c there is 1 possible solution
- use The Law of Sines to solve for angle C
- use the Sum of Angles Rule to find the other angle, B
- use The Law of Sines to solve for the last side, b
- Example:
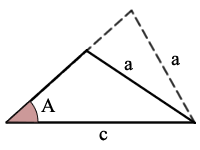
If a < c we have 3 potential situations. "If sin(A) < a/c, there are two possible triangles satisfying the given conditions. If sin(A) = a/c, there is one possible triangle. If sin(A) > a/c, there are no possible triangles." [1]
sin(A) < a/c, there are two possible triangles
solve for the 2 possible values of the 3rd side b = c*cos(A) ± √[ a2 - c2 sin2 (A) ][1]
for each set of solutions, use The Law of Cosines to solve for each of the other two angles
present 2 full solutions
Example:
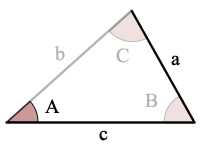
sin(A) = a/c, there is one possible triangle
use The Law of Sines to solve for an angle, C
use the Sum of Angles Rule to find the other angle, B
use The Law of Sines to solve for the last side, b
Example:
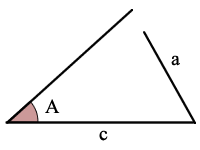
sin(A) > a/c, there are no possible triangles
Error Notice: sin(A) > a/c so there are no solutions and no triangle!
Example:
SAS is Side, Angle, Side
Given the size of 2 sides (c and a) and the size of the angle B that is in between those 2 sides you can calculate the sizes of the remaining 1 side and 2 angles.
use The Law of Cosines to solve for the remaining side, b
determine which side, a or c, is smallest and use the Law of Sines to solve for the size of the opposite angle, A or C respectively.[2]
use the Sum of Angles Rule to find the last angle
SSS is Side, Side, Side
Given the sizes of the 3 sides you can calculate the sizes of all 3 angles in the triangle.
use The Law of Cosines to solve for the angles. You could also use the Sum of Angles Rule to find the final angle once you know 2 of them.
Sum of Angles in a Triangle
In Degrees A + B + C = 180°
In Radians A + B + C = π
Law of Sines
If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of sines states:
a/sin A = b/sin B = c/sin C
Solving, for example, for an angle, A = sin-1 [ a*sin(B) / b ]
Law of Cosines
If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of cosines states:
a2 = c2 + b2 - 2bc cos A, solving for cos A, cos A = ( b2 + c2 - a2 ) / 2bc
b2 = a2 + c2 - 2ca cos B, solving for cos B, cos B = ( c2 + a2 - b2 ) / 2ca
c2 = b2 + a2 - 2ab cos C, solving for cos C, cos C = ( a2 + b2 - c2 ) / 2ab
Solving, for example, for an angle, A = cos-1 [ ( b2 + c2 - a2 ) / 2bc ]
Other Triangle Characteristics
Triangle perimeter, P = a + b + c
Triangle semi-perimeter, s = 0.5 * (a + b + c)
Triangle area, K = √[ s*(s-a)*(s-b)*(s-c)]
Radius of inscribed circle in the triangle, r = √[ (s-a)*(s-b)*(s-c) / s ]
Radius of circumscribed circle around triangle, R = (abc) / (4K)
References/ Further Reading
[1] Weisstein, Eric W. "ASS Theorem." From MathWorld-- A Wolfram Web Resource. ASS Theorem.
[2] Math is Fun - Solving SAS Triangles
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.
Weisstein, Eric W. "Triangle Properties." From MathWorld-- A Wolfram Web Resource. Triangle Properties.
Math is Fun at Solving Triangles.
Find All Solutions to Each of the Following Triabgles
Source: https://www.calculatorsoup.com/calculators/geometry-plane/triangle-theorems.php